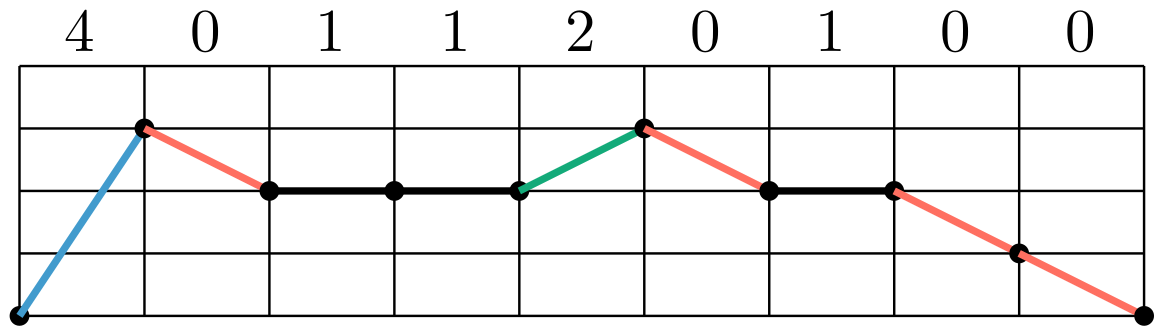
Illustration

To illustrate our result, the 30 Lukasiewicz words with content {0,0,0,1,2,3} are displayed below in the order generated by our algorithm. The arrow on top of each Lukasiewicz word illustrates the left-shift used to transform the Lukasiewicz word into its successor: in the first row, shifts the 2 to the front of the string to generate 230100, the string in the next row.

Successor Rule

The strings in this figure are generated by a simple rule. First, we define the non-increasing prefix of a Łukasiewicz word to be the longest prefix of the string such that each symbol in the prefix is at most as large as the symbol before it. Unsurprisingly, this results in a prefix of the string that does not contain any 'increases' (from left to right) beteween successive symbols. For example, the non-increasing prefix of 320010 is 3200, as it is the longest prefix of 320010 that does not contain any increases. We will refer to the non increasing prefix of a string as ρ, the length of ρ as m, and the sum of all symbols in ρ as Σ(ρ). Given this definition, repeatedly applying the following rule to a Łukasiewicz word will generate wll Łukasiewicz words with its set of content.

Let a=a1,a2,...,an be a Lukasiewicz word of length n. To generate all Lukasiewicz words with the same content set as a, repeatedly apply the following successor rule, next(a).

As a example, let's consider applying next(a) to the first couple strings in the illustration.

next(302100): 302100 has non-increasing prefix 30 with length 2.

• m ≠ n, so case 4a is not applied.
• am < am+2, the second condition in case 4b, is true:
m=2, a2=0,a4=1,, therefore am < am+2

Therefore, case 4b is applied: left(1,3) applied to 302100. This shifts the 2 to position 1 and genereates 230100

next(230100): 230100 has non-increasing prefix 3 with length 1.

• m ≠ n, so case 4a is not applied.
• None of the conditions in case 4b are true: m ≠ n-1, am = 2 > am+2 = 0, Σ(ρ)=2; m=1; 2>1
• The condition in case 4c is not true: am+2 = 0

Therefore, case 4d is applied: left(2,3) is applied to 230100. This shifts the 0 into the second position, yielding 203100.

Repeatedly following this process will generate all Lukasiewicz words with content {0,0,0,1,2,3}.

Observations

A notable property of this successor rule is that it always shifts positive symbols to position 1 and zeroes to position 2. The successor rule can therefore be restated as the following two step process:

Find the symbol to shift

• If the non increasing prefix has length at least n-1, shift the last symbol
• If am < am+2, or (am+2 == 0 and Σ(ρ) == m) then shift symbol m+1
• Otherwise, shift symbol m+2

Find the location to shift it to

• If the symbol being shifted is equal to zero, shift it to position 2
• Otherwise, shift it to position 1

Implementation

Goals

• Efficiency: O(1) time per generated string. In particular, we would like to achieve a loopless implementation, which uses worst case O(1) time per generated string. This is a higher goal than constant amortized time, which takes average O(1) time per string, but individual strings may (infrequently) require O(n) time to generate.
• Simplicity: We would like our code to be simple and readable.

Challenges

• m,ρ,Σ(ρ): In theory, finding the length and sum of the non-increasing prefix of a string is a non-constant time operation: it varies based on the length of the non-increasing prefix, which can be up to n symbols long.
• left(i,j): In an array based representation of a Lukasiewicz word, shifting a symbol left with no guarantee on length of the shift or the content of the first j symbols of the string would be a non-constant time operation. In the worst case, left(1,n) would require moving each of the first n-1 symbols of the string down one position.
• Knowing when to stop: Our successor rule gives a way to go from one symbol to the next

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Praesent facilisis quam velit, vitae feugiat sapien lacinia non. Nulla in libero vitae risus tincidunt vestibulum sodales eu ante. Donec id lacinia ipsum. Nam pellentesque lacinia suscipit. Duis maximus metus vitae volutpat laoreet. Nulla facilisi. Ut sit amet nibh orci. Nulla nunc arcu, luctus id quam a, facilisis rhoncus dui. Aliquam egestas commodo nulla a eleifend. Quisque enim nisl, tempus pellentesque elementum eu, faucibus placerat mi. Etiam egestas tristique dapibus. Duis ultricies nisi et rutrum blandit. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. In hendrerit est eros, nec dapibus leo volutpat ultrices. Nulla a est sed quam venenatis placerat. Nullam commodo, diam et congue pellentesque, odio tellus tristique quam, varius eleifend elit magna nec sem. Donec id arcu id dolor elementum lacinia a eget mauris. Sed porttitor metus eu feugiat lacinia. Aliquam erat volutpat. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Vivamus nunc elit, ultricies a metus eget, malesuada tincidunt sem. Aliquam dolor mi, euismod quis aliquam et, dignissim non erat. Duis massa tellus, porttitor id turpis convallis, tempus vehicula urna. Nam ac mollis magna, at dapibus nunc. Vestibulum tristique euismod fermentum. Maecenas sed sapien cursus, condimentum quam ut, faucibus massa. Etiam sit amet varius urna. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Fusce consectetur tincidunt erat, vel viverra velit rhoncus a. Mauris molestie varius dolor, quis ultricies nunc finibus non. Etiam facilisis odio ac imperdiet tempus. Donec vitae lectus egestas, elementum ante at, maximus urna. Vestibulum dictum, neque in ornare tincidunt, mi eros gravida leo, sit amet consequat orci ex ac leo. Sed a consequat orci. Fusce sed tempus ex. Duis ut dui pharetra, viverra arcu sed, sodales velit. Phasellus metus justo, fringilla eget facilisis quis, fringilla eget leo. Integer in fringilla massa, ac vehicula mi. Suspendisse maximus dolor eget leo gravida accumsan. Sed et placerat ante, vel tincidunt tellus. Curabitur varius eget nisi eget auctor. Donec nisl ex, condimentum ac ex a, tempus pretium velit. In venenatis, massa rutrum placerat lacinia, justo dolor vestibulum tortor, sit amet condimentum nisl nunc eu justo. Cras nunc dolor, elementum ac mi sit amet, auctor eleifend quam. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Phasellus ornare est mi, ut ornare enim bibendum et. Nulla nisi massa, euismod id sem a, convallis tincidunt nulla. Nulla aliquet augue velit, aliquam fringilla nisi scelerisque quis. Praesent pharetra scelerisque mattis. Sed mollis porta arcu in mollis. Aenean finibus massa a rutrum ultrices. Duis fermentum sollicitudin ultrices. Quisque congue turpis vitae lacus iaculis, vitae tempus nisl vestibulum. Ut euismod nulla metus, at mattis ipsum lacinia eu. Nullam sed lectus ac mauris auctor laoreet vel et urna. Quisque placerat erat turpis, iaculis euismod risus dapibus eget. Etiam pharetra est ante, in varius erat laoreet non. Curabitur at auctor diam. Sed dui odio, sagittis vitae ligula vel, euismod vehicula sem. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Duis efficitur ultrices ligula, eu dignissim nisl venenatis eu. Mauris nisi justo, blandit sit amet venenatis volutpat, cursus in metus. Aenean eros augue, laoreet a quam sit amet, feugiat pellentesque nibh. Aliquam erat volutpat.